Participating and Finishing Advent of Code 2019 (a.k.a. Intcode Odyssey)
Advent of code
I took part in Advent of Code 2019 (often shortened to AOC), a game that challenges participants to a two-part puzzle every day in December until the 25th.
I had finished the 2017 edition and participated in the 2018 one (where I "burned out" after 19 days), so I was eager to try again in 2019.
Participating turned out to be quite a lot of work, but also a lot of excitement. I wrote my solutions using Python (as people who know me would expect) with the code available on my Github repo. In most cases, I was able to solve the problems by myself. When stuck, I found it helpful to discuss the problems with my awesome colleague TFO. For the harder problems towards the end, I peeked at the AOC Subreddit and at a well written Python walkthrough by Github user mebeim.
 The finished calendar, obtained after getting 50 stars, i.e. completing 50 puzzle problems.
The finished calendar, obtained after getting 50 stars, i.e. completing 50 puzzle problems.
What were the problems about?
I'll try to give a short classifications of the problem types encountered below. Difficulty is relative to my current skills, so this probably doesn't easily transfer to anyone else.
Also, every other day featured an Intcode computer problem (a type of Virtual Machine) which led to successive implementations: more opcodes, relative base, extra memory, ASCII inputs and outputs. It also led to many different applications running on the opcode computer, most notably an Arkanoid clone.
| Day | Problem type | Difficulty |
|---|---|---|
| 1 | Arithmetic | Easy |
| 2 | Intcode | Easy |
| 3 | Grids | Easy |
| 4 | String matching | Easy |
| 5 | Intcode with parameter mode and more opcodes | Easy |
| 6 | Graphs | Easy |
| 7 | Intcode with combinatorials | Medium |
| 8 | 3D arrays | Easy |
| 9 | Intcode with relative mode and more opcodes | Medium |
| 10 | Geometry | Easy |
| 11 | Intcode with painting robot | Easy |
| 12 | Physics style with moons | Medium |
| 13 | Intcode playing Arkanoid | Medium |
| 14 | Chemistry style problem | Hard |
| 15 | Intcode Maze exploration | Medium |
| 16 | FFT with a twist | Medium |
| 17 | ASCII Intcode computer with a grid-rover | Hard |
| 18 | Recursive shortest path exploration | Hard |
| 19 | Intcode Grid-based problem | Easy |
| 20 | Shortest paths in a recursive maze | Hard |
| 21 | Meta Intcode programming using logic | Hard |
| 22 | Arithmetic with large primer numbers | Hard |
| 23 | Intcode cluster computer | Easy |
| 24 | Recursive game of life | Medium |
| 25 | Interactive maze discovery with Knapsack | Medium |
Looking at my personal stats, the level of difficulty is well-correlated with the time it took me to solve the problem, especially part 2.
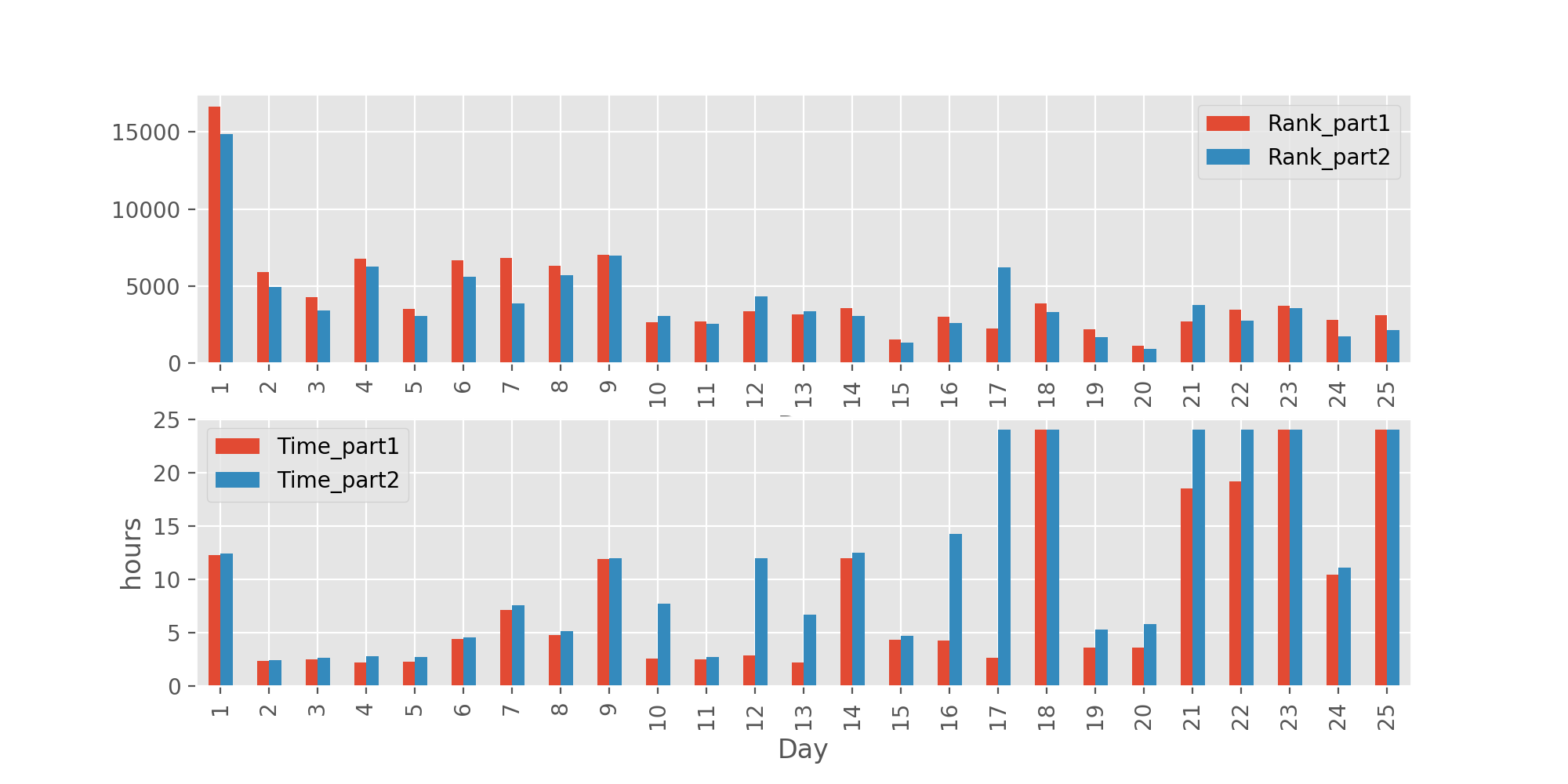 Ranking and time it took me to solve the problems.
Ranking and time it took me to solve the problems.
For me, the two hardest problems were 18 and 22. Puzzle 18 was hard for me because I had to write a recursive solution, and I am not good at that. Problem 22 was hard because it involved modular arithmetic way beyond my skills. Luckily, the AOC Subreddit provided helpful pointers that allowed me to solve these problems too.
A Gallery of Visualizations
The different problems led, more often than not, to interesting visualizations while working out the solutions. Here's a collage of some of these I collected. My favorite from these shows a state of the Arkanoid clone running on the Intcode computer and controls I built with ipywidgets to play the game.
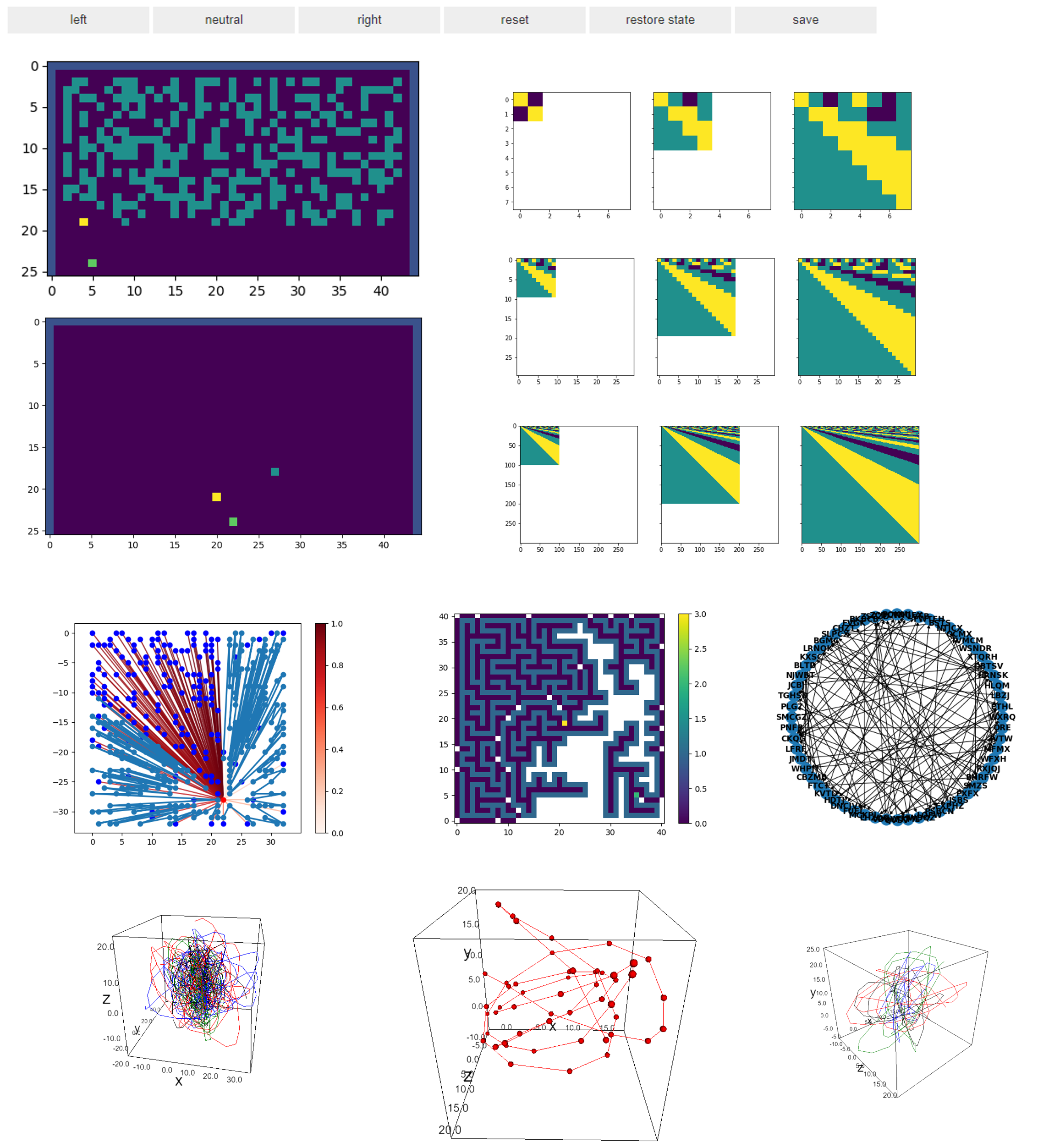 A collage of AOC 2019 visualizations.
A collage of AOC 2019 visualizations.
Python lessons learnt
Since this year featured a lot of graph problems, I came up with a way of building graphs that I found quite helpful and that I will certainly use again in the future.
It consists of the following: building a dictionary that holds node coordinates in the form of complex numbers (or tuples of (r, c) coordinates). Then making a graph in two steps: adding the nodes first and then computing adjacent nodes that can easily be checked if they are present or not (since a Graph is a hashmap).
This led to the following code:
import networkx as nx
def build_graph(environment):
G = nx.Graph()
# first pass: add nodes to graph
for coord, blockval in environment.items():
if blockval != 0:
G.add_node(coord)
# second pass: connect them by using complex number addition
for node in G:
for direction in [1, 1j, -1, -1j]:
other = node + direction
if other in G:
G.add_edge(node, other)
return G
The Future
I hugely enjoyed Advent of Code 2019. Many thanks to its creator, Eric Wastl. I can only hope that I'll be able to participate again, hopefully with a new language (because I've been using Python for ten years now ^^ and I feel ready for an additional challenge).