Plotting the World Oil Reserves
Have you ever seen this plot?
from IPython.display import Image
Image(url='http://planetforlife.com/images/growinggap.jpg')
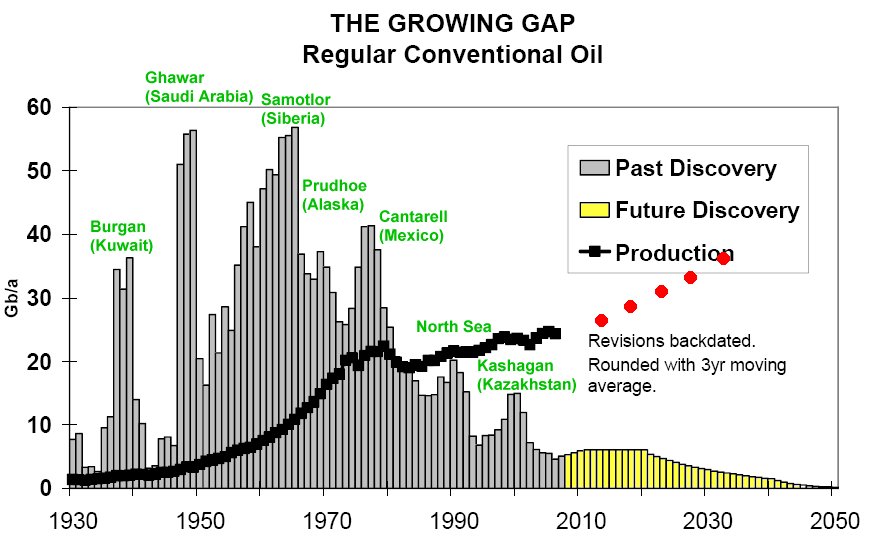
What this plot shows are historical discoveries of regular conventional oil (aka "oil fields") and production (aka "taking oil out of the oil field"). People who try to understand the world often think about this problem when they consider how much our current way of life is based on oil.
Ever since I first saw a version of this plot in a talk (this one), I've been wondering about this fascinating data. Since there is an oil field list page on Wikipedia, let's try to see if we can roughly replicate this curve.
Oil fields on Wikipedia¶
The data for oil fields can be found here: https://en.wikipedia.org/wiki/List_of_oil_fields. Let's download the data and parse it into a table. We can do this with a little bit of manual fiddling using requests, beautifulsoup and pandas.
import requests
from bs4 import BeautifulSoup
import pandas as pd
r = requests.get('https://en.wikipedia.org/wiki/List_of_oil_fields')
tree = BeautifulSoup(r.text, 'html.parser')
table = tree.find('table', class_='wikitable')
df = pd.read_html(str(table), header=0)[0]
df.head()
| Field | Location | Discovered | Started production | Peaked | Recoverable oil, past and future (billion barrels) | Production (million barrels/day) | Rate of decline | |
|---|---|---|---|---|---|---|---|---|
| 0 | Ghawar Field | Saudi Arabia | 1948[3] | 1951[3] | 2005,[4] disputed[5] | 88-104[6] | 5[7] | 8% per year[8] |
| 1 | Burgan Field | Kuwait | 1937 | 1948 | 2005[9] | 66-72[8] | 1.7[10] | 14% per year[citation needed] |
| 2 | Ahvaz Field | Iran | 1958 | NaN | 1970s[11] | 65 (25 recoverable)[12] | .750[13] | NaN |
| 3 | Upper Zakum oil field | Abu Dhabi, UAE | 1963[14] | 1982[15][16] (1967[14]) | Production still increasing | 50[15] (21 recoverable[14]) | 0.750[15] | Extension planned to 1 MMb/d[17] |
| 4 | Gachsaran Field | Iran | 1927 | 1930 | 1974 | 66[18] | 0.480 | NaN |
Analysis¶
Now that we have this list of oil fields, we can do some elementary plot by country and year discovered.
By country¶
import holoviews as hv
hv.extension('bokeh')
%%opts Bars [width=600 tools=['hover'] xrotation=45]
hv.Bars(df.groupby('Location').agg('count')['Field'])
However, as you can see in the above plot, some labels are not adequate and repeat the countries several times. Let's clean this up by replacing each country with its nearest neighbor from a list of world countries.
import pycountry
from difflib import SequenceMatcher
def similar(a, b):
return SequenceMatcher(None, a, b).ratio()
def match_country(c):
countries = list(country.name for country in pycountry.countries)
full_name = [c in other.name or other.name in c for other in pycountry.countries]
alpha3 = [c in other.alpha_3 or other.alpha_3 in c for other in pycountry.countries]
alpha2 = [c in other.alpha_2 or other.alpha_2 in c for other in pycountry.countries]
if any(full_name):
return list(pycountry.countries)[full_name.index(True)].name
elif any(alpha3):
return list(pycountry.countries)[alpha3.index(True)].name
elif any(alpha2):
return list(pycountry.countries)[alpha2.index(True)].name
else:
# difflib
return max(((co, similar(c, co)) for co in countries), key=lambda item: item[1])[0]
df.Location = [match_country(c) for c in df.Location]
%%opts Bars [width=600 height=500 tools=['hover'] xrotation=45]
hv.Bars(df.groupby('Location').agg('count')['Field'].sort_values())
The above plot nicely shows the key players in the oil market: Russia and the Gulf states.
By discovery year¶
We also need to clean up the data of discovery year. We will do so using a regular expression.
df.Discovered = pd.to_numeric(df.Discovered.str.extract('(\d{4})', expand=False))
%%opts Bars [width=600 height=500 tools=['hover'] xrotation=45]
hv.Bars(df.groupby('Discovered').agg('count')['Field'])
Here the trend is not yet apparent. Let's regroup these by ten year bins.
import numpy as np
hist, bin_edges = np.histogram(df.Discovered.dropna().values, range=(1880, 2020), bins=14)
%%opts Bars [width=600 height=500 tools=['hover'] xrotation=45]
hv.Bars((bin_edges, hist), kdims='Decade discovered', vdims='number of oil fields')
So it seems indeed that the amount of oil fields discovered has been on the decline for quite a long time.
Analysis of the amount of oil¶
However, what really matters is the amount of oil discovered. Can we also do this? To achieve that, we need to extract the amount of oil from our table.
We first need to clean up the data a little bit.
df['Recoverable oil'] = pd.to_numeric(
df['Recoverable oil, past and future (billion barrels)'].str.extract('(\d+(?:\.\d+)?)', expand=False))
Let's plot the data in billion barrels, first per country, then per decade discovered.
By country¶
%%opts Bars [width=600 height=500 tools=['hover'] xrotation=45]
hv.Bars(df[['Location', 'Recoverable oil']].groupby('Location').agg('sum').sort_values(by='Recoverable oil'))
By discovery year¶
subdf = df[['Discovered', 'Recoverable oil']].dropna()
hist, bin_edges = np.histogram(subdf['Discovered'].values,
range=(1880, 2020), bins=14, weights=subdf['Recoverable oil'])
%%opts Bars [width=600 height=500 tools=['hover'] xrotation=45]
hv.Bars((bin_edges, hist), kdims='Decade discovered', vdims='Billions of barrels')
Again, we see a sharp drop in discoveries since at least three decades. This could very possibly mean that the age of big oil field discoveries is over.
Forecasting using the Hubbert curve¶
Of course, we would like to have an idea for how long the production can adapt to the worldwide oil demand. To do that, we can use the Hubbert model (as in the famous Hubbert curve) to fit the data we have gathered and give some predictions about world oil production.
First, let's take a look at the Hubbert model itself.
The Hubbert model¶
The Hubbert model proposes a parametric form for the cumulative extracted oil as a function of time described by the following equation (primary reference for this is here):
$$ Q(t) = \frac{Q_{\infty}}{1 + \exp(-\omega (t - \tau))} $$
The parameter $Q_{\infty}$ gives the total quantity of oil you can extract from a well and $\tau$ defines the peak extraction time of the oil (as well as the point when you have extracted half of the existing capacity). $t$ is then the time (in years for our purposes). Finally, $\omega$ is a parameter that describes how fast or how slowly the oil is extracted.
Let's have a quick look at the cumulative production curve.
def hubbert_cumprod(qinf, omega, t, tau):
"""Hubbert cumulative production function."""
return qinf / (1 + np.exp(-omega * (t - tau)))
tau = 5
t = np.linspace(-10, 30, num=200)
cumprod = hubbert_cumprod(1, 0.5, t, tau)
cumprod_plot = hv.Curve((t, cumprod), kdims='time', vdims='cumulative production').opts(width=300)
tau_plot = hv.VLine(tau, label='tau')
cumprod_plot * tau_plot
The time derivative of the cumulative production is the instantaneous production, the production at a given moment in time. We can plot it alongside the previous graph.
def hubbert_prod(qinf, omega, t, tau):
"""Hubbert instantaneous production function."""
return qinf * omega / (np.exp(-omega / 2. * (t - tau)) + np.exp(omega / 2. * (t - tau)))**2
prod = hubbert_prod(1, 0.5, t, tau)
prod_plot = hv.Curve((t, prod), kdims='time', vdims='instantaneous production').opts(width=300)
(cumprod_plot * tau_plot + prod_plot * tau_plot)
Fitting the model to our data¶
Now of course, the question is: how do we use that model and our data that we have used in the above section together? I propose the following: we fit the time dynamics corresponding to the $\omega$ parameter using the average world data and then use this to do some forecasting.
A simple strategy for this fit is to use the data on the peak production associated to the oil fields. Some of the fields give a starting data as well as a peak date. For instance the Ghawar Field in Saudi Arabia has the following data:
df.loc[0]
Field Ghawar Field Location Saudi Arabia Discovered 1948 Started production 1951[3] Peaked 2005,[4] disputed[5] Recoverable oil, past and future (billion barrels) 88-104[6] Production (million barrels/day) 5[7] Rate of decline 8% per year[8] Recoverable oil 88 Name: 0, dtype: object
The field started production in 1951, peaked in 2005 (even though this is disputed) and has a total recoverable oil quantity of at least 88 billion barrels. This means we can fit the production data using the current production of 5 million barrels per day. Since our units is billion barrels for the reserve, we will convert this production value to billion barrels per year:
5e6 * 365 * 1e-9
1.8250000000000002
We can then fit the $\omega$ value at time $t = \tau + n$ where $n$ is the number of years since the peak using this formula:
$$ P(t=\tau + n) = \frac {\omega Q_{\infty}} {(\exp(\omega n /2 ) + \exp(-\omega n /2 ))^2} $$
Here $n$ is approximately 15 years and $Q_{\infty}$ 88 billion barrels.
from scipy.optimize import curve_fit
curve_fit(lambda n, omega: omega * 88 / (np.exp(omega * n / 2) + np.exp(- omega * n / 2))**2,
xdata = [15.],
ydata= [1.82],
p0=0.1)
/Users/kappamaki/anaconda/lib/python3.6/site-packages/scipy/optimize/minpack.py:787: OptimizeWarning: Covariance of the parameters could not be estimated category=OptimizeWarning)
(array([0.1028937]), array([[inf]]))
Let's see if the data we get is the one we expect:
tau = 2005
omega = 0.1028
Q = 88
t = np.linspace(1951, 2051, num=200)
cumprod = hubbert_cumprod(Q, omega, t, tau)
prod = hubbert_prod(Q, omega, t, tau)
cumprod_plot = hv.Curve((t, cumprod), kdims='time', vdims='cumulative production', label='model')
tau_plot = hv.VLine(tau, label='tau')
prod_plot = hv.Curve((t, prod), kdims='time', vdims='instantaneous production', label='model')
data_point = hv.Points((2019, 1.82), label='data point').options(size=10)
%%opts Curve [tools=['hover'] width=600] Overlay [legend_position='top_left']
prod_plot * tau_plot * data_point
Of course, this fit is not very good. But I can't think of a better way than just this simple point estimate.
We can move on and do this fit on the other oil fields that have the complete data: recoverable oil, peak year and current production. A little more of data munging is needed:
df['Peak'] = df['Peaked'].str.extract('(\d{4})', expand=False)
df['n'] = pd.datetime(2019, 1, 1) - pd.to_datetime(df['Peak'])
df['Production'] = df['Production (million barrels/day)'].str.extract('(\d*\.?\d*)', expand=False)
df.head()
| Field | Location | Discovered | Started production | Peaked | Recoverable oil, past and future (billion barrels) | Production (million barrels/day) | Rate of decline | Recoverable oil | Peak | n | Production | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Ghawar Field | Saudi Arabia | 1948.0 | 1951[3] | 2005,[4] disputed[5] | 88-104[6] | 5[7] | 8% per year[8] | 88.0 | 2005 | 5113 days | 5 |
| 1 | Burgan Field | Kuwait | 1937.0 | 1948 | 2005[9] | 66-72[8] | 1.7[10] | 14% per year[citation needed] | 66.0 | 2005 | 5113 days | 1.7 |
| 2 | Ahvaz Field | Iran, Islamic Republic of | 1958.0 | NaN | 1970s[11] | 65 (25 recoverable)[12] | .750[13] | NaN | 65.0 | 1970 | 17897 days | .750 |
| 3 | Upper Zakum oil field | United Arab Emirates | 1963.0 | 1982[15][16] (1967[14]) | Production still increasing | 50[15] (21 recoverable[14]) | 0.750[15] | Extension planned to 1 MMb/d[17] | 50.0 | NaN | NaT | 0.750 |
| 4 | Gachsaran Field | Iran, Islamic Republic of | 1927.0 | 1930 | 1974 | 66[18] | 0.480 | NaN | 66.0 | 1974 | 16436 days | 0.480 |
Let's drop the fields that don't have enough data:
fit_data = df[['Field', 'Location', 'Discovered', 'Recoverable oil', 'Peak', 'n', 'Production']].dropna()
fit_data['Production'] = pd.to_numeric(fit_data['Production'])
fit_data = fit_data.reset_index(drop=True)
fit_data
| Field | Location | Discovered | Recoverable oil | Peak | n | Production | |
|---|---|---|---|---|---|---|---|
| 0 | Ghawar Field | Saudi Arabia | 1948.0 | 88.0 | 2005 | 5113 days | 5.000 |
| 1 | Burgan Field | Kuwait | 1937.0 | 66.0 | 2005 | 5113 days | 1.700 |
| 2 | Ahvaz Field | Iran, Islamic Republic of | 1958.0 | 65.0 | 1970 | 17897 days | 0.750 |
| 3 | Gachsaran Field | Iran, Islamic Republic of | 1927.0 | 66.0 | 1974 | 16436 days | 0.480 |
| 4 | Cantarell Field | Mexico | 1976.0 | 35.0 | 2004 | 5479 days | 0.340 |
| 5 | Tengiz Field | Kazakhstan | 1979.0 | 26.0 | 2010 | 3287 days | 0.530 |
| 6 | Samotlor Field | Russian Federation | 1965.0 | 14.0 | 1980 | 14245 days | 0.844 |
| 7 | Prudhoe Bay | United States | 1967.0 | 25.0 | 1988 | 11323 days | 0.660 |
| 8 | Ekofisk oil field | Norway | 1969.0 | 3.3 | 2006 | 4748 days | 0.127 |
Let's now loop over this table and fit the omega values.
from functools import partial
def fit_func(n, omega, Q):
return omega * Q / (np.exp(omega * n / 2) + np.exp(- omega * n / 2))**2
omegas = []
model_production = []
for ind, series in fit_data.iterrows():
Q = series['Recoverable oil']
n = series.n.days / 365
prod = series.Production
fit = curve_fit(partial(fit_func, Q=Q),
xdata = [n],
ydata= [1.82],
p0=0.1)
omegas.append(fit[0][0])
model_production.append(fit_func(n, omegas[-1], Q))
fit_data['omega'] = omegas
fit_data['model_production'] = model_production
/Users/kappamaki/anaconda/lib/python3.6/site-packages/scipy/optimize/minpack.py:787: OptimizeWarning: Covariance of the parameters could not be estimated category=OptimizeWarning)
fit_data[['Field', 'Production', 'model_production']]
| Field | Production | model_production | |
|---|---|---|---|
| 0 | Ghawar Field | 5.000 | 1.406367 |
| 1 | Burgan Field | 1.700 | 1.054775 |
| 2 | Ahvaz Field | 0.750 | 0.296773 |
| 3 | Gachsaran Field | 0.480 | 0.328125 |
| 4 | Cantarell Field | 0.340 | 0.521986 |
| 5 | Tengiz Field | 0.530 | 0.646347 |
| 6 | Samotlor Field | 0.844 | 0.080308 |
| 7 | Prudhoe Bay | 0.660 | 0.180414 |
| 8 | Ekofisk oil field | 0.127 | 0.056793 |
If we compare the model predictions as well as the real values, we can see that the point-fit is not really a good method (in the sense that it doesn't fit the data really well).
But at least, we now have some values for the $\omega$ parameter. So we can turn to forecasting oil reserves as a function of time, using the average omega value.
Forecasting using the Hubbert model¶
Our final plot will be simple: using an average value for the omega parameter, we can plot the yearly oil production in billion of barrels as a function of time under the assumption that all oil fields follow the Hubbert model.
mean_omega = fit_data.omega.mean()
subdf = df[['Field', 'Discovered', 'Peak', 'Recoverable oil']].copy()
subdf['Peak'] = pd.to_numeric(subdf['Peak'])
subdf['UntilPeak'] = (subdf['Peak'] - subdf['Discovered'])
subdf.UntilPeak = subdf.UntilPeak.fillna(value=subdf.UntilPeak.median())
subdf.loc[np.isnan(subdf.Peak), 'Peak'] = subdf[np.isnan(subdf.Peak)].Discovered + subdf[np.isnan(subdf.Peak)].UntilPeak
subdf.head()
| Field | Discovered | Peak | Recoverable oil | UntilPeak | |
|---|---|---|---|---|---|
| 0 | Ghawar Field | 1948.0 | 2005.0 | 88.0 | 57.0 |
| 1 | Burgan Field | 1937.0 | 2005.0 | 66.0 | 68.0 |
| 2 | Ahvaz Field | 1958.0 | 1970.0 | 65.0 | 12.0 |
| 3 | Upper Zakum oil field | 1963.0 | 1987.0 | 50.0 | 24.0 |
| 4 | Gachsaran Field | 1927.0 | 1974.0 | 66.0 | 47.0 |
t = np.arange(1880, 2080)
total_production = np.zeros_like(t, dtype=np.float)
curves = []
for ind, series in subdf.dropna().iterrows():
field_production = hubbert_prod(series['Recoverable oil'], mean_omega, t, series['Peak'])
total_production += field_production
curves.append(hv.Curve((t, field_production), label=series.Field, kdims='year', vdims='billion barrels'))
%%opts Curve [width=600 tools=['hover']]
hv.Overlay(curves)
And finally, we can show the total production over the years computed using this data as well as the cumulative production.
%%opts Curve [tools=['hover']]
hv.Curve((t, total_production), kdims='year', vdims='billion barrels', label='yearly production').opts(width=300) + \
hv.Curve((t, total_production.cumsum()), kdims='year', vdims='cumulated billion barrels', label='cumulative production').opts(width=300)
Are these curves realistic? Well, probably not. In particular, they don't look like the data that I cited at the beginning of this article. Does that mean that the model we used to describe this situation is wrong? Yes, very probably (or our fit procedure, of course)! However, it is still usefull in the sense that it gives a numerical estimate of the world oil production from first principles as well as its dynamics.
Conclusions¶
I hope you had fun following along this data exploration. While the first parts were simply descriptive, we tried to apply some basic modeling to the publicly available data. I don't think the result is very good, but it nonetheless is an interesting approach to get to know some of basic data related to oil fields.
This post was entirely written using the IPython notebook. Its content is BSD-licensed. You can see a static view or download this notebook with the help of nbviewer at 20190102_OilFieldsWikipedia.ipynb.